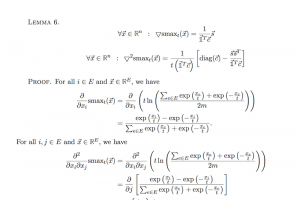Un groupe de chercheurs de l'Institut de technologie du Massachusetts (MIT) a mis au point une solution potentiellement plus efficace pour aider les ordinateurs à résoudre certains problèmes complexes d'optimisation. « Le nouvel algorithme est informatiquement plus efficace que d'autres approches, parce qu'il travaille en mode quasi linéaire », a expliqué Jonathan Kelner, professeur agrégé de mathématiques appliquées au MIT, membre du Computer Science and Artificial Intelligence Laboratory et par ailleurs coauteur de l'algorithme. « Pour ce type de calcul, les temps d'exécutions des algorithmes existants sont très insuffisants, comparés à ce que l'on peut obtenir avec des algorithmes linéaires », a indiqué le chercheur par courriel. En fait, quand un problème devient plus complexe, les performances de l'ordinateur sont considérablement ralenties, parce qu'il met plus de temps à le résoudre.
L'échelle linéaire signifie que le temps nécessaire pour résoudre un problème avec un algorithme est plus ou moins directement proportionnel à l'ampleur du problème à résoudre. La puissance du nouvel algorithme pourrait avoir d'importantes répercussions pour l'industrie, notamment si celui-ci permet de réduire considérablement la quantité de travail nécessaire pour écrire un code de programme et s'il permet aux ordinateurs de traiter efficacement des problèmes complexes. Par exemple, une compagnie aérienne pourrait utiliser le nouvel algorithme pour trouver le moyen le plus efficace de gérer ses équipages. Ou encore, un routeur pourrait l'utiliser pour calculer le chemin le plus rapide pour faire circuler des données sur un réseau encombré (voir illustration ci-dessus).
Un algorithme pour l'instant baptisé KLOS
Jonathan Kelner et son collègue, le chercheur Lorenzo Orecchia, ont présenté leur algorithme au cours du Symposium ACM-SIAM of Discrete Algorithms organisé par l'Association of Computing Machinery (ACM) qui s'est tenu à Portland (5-7 janvier 2014). De nombreux étudiants des cycles supérieurs et des mathématiciens de l'Université de Yale et de l'Université de Californie du Sud ont également participé aux travaux. Un article sur le sujet a également été publié dans le journal Discrete Algorithms du Symposium ACM-SIAM (édition de janvier 2014). Il a remporté le prix du meilleur article de l'ACM-SIAM publié cette année. L'algorithme n'a pas encore de nom officiel, mais il est désigné sous le nom « d'algorithme KLOS », d'après les premières lettres des noms des principaux auteurs (Jonathan Kelner, Yin Lee Tat, Lorenzo Orecchia et Aaron Sidford, tous chercheurs du MIT).
Aujourd'hui, les problèmes d'optimisation sont généralement résolus en utilisant des algorithmes de flot maximum ou max-flow. Le problème du flot maximum est le suivant : « Étant donné un graphe orienté G(V,E), où chaque arête u,v a une capacité c(u,v), on cherche un flot maximum f depuis la source s vers le puits t, sous contrainte de capacité » (source Wikipédia). Le flot maximum modélise donc un réseau sous forme de graphe où tous les points finaux sont représentés comme des noeuds, ou des « vertices », et toutes leurs connexions sont représentées comme des arêtes. Il calcule ensuite le moyen le plus efficace d'acheminer le trafic à travers le réseau, compte tenu de la capacité maximale de chaque noeud. Le flot maximum calcule le débit sur les arêtes en saturant chaque arête une à une, passant d'une arête à l'autre pour avoir plus de débit. « Dans les réseaux très complexes, cette approche demande trop de temps et trop de ressources pour être efficace. Les problèmes actuels mettent souvent en jeu des millions, voire des milliards d'arêtes », fait remarquer Jonathan Kelner.
Le nouvel algorithme teste tous les chemins, ou toutes les arêtes en même temps. « L'approche ressemble un peu à celle d'un courant électrique qui traverserait un circuit de résistances en parallèle, et prendrait tous les chemins possibles à la fois ». Pour réduire encore plus le temps de traitement, l'algorithme peut identifier les goulets d'étranglement dans le réseau, ce que ne font généralement pas les algorithmes de flot maximum.